Chapitre 4 : Continuité et dérivation
Exercice "VRAI ou FAUX"Pour toute fonction réelle f et pour tout réel x0, on a:
f est continue en x0.gif)
f est continue en x0
Vrai Faux
.gif)
Exercice "VRAI ou FAUX"Pour toute fonction réelle f et pour tout réel x0, on a:
f continue à gauche en x0.gif)
f continue à gauche en x0
Vrai Faux
Sélection multiple
Les
fonctions suivantes sont bien continues sur leur domaine de definition :
Les
fonctions polynomiales | |
La
fonction partie entière | |
La
fonction valeur absolue | |
Les
fonctions rationnelles | |
La
fonction tan(x) | |
Sélection multiple
Le
théorème des valeurs intermédiaires étendu veut dire que, dans le cadre d'une fonction f continue sur un intervalle [a,b], :
Toute
valeur intermédiaire entre a et b est l’antécédent d’au moins un élément de [f(a),f(b)] | |
Toute
valeur intermédiaire entre f(a) et (b) est l’image d’au moins un élément de
[a,b] | |
Si f(a) et f(b) sont de signes opposés, alors f
s’annule en au moins un point de l’intervalle ]a,b[ | |
Exercice "VRAI ou FAUX"Pour toute fonction f continue sur un intervalle non vide I, on a:
f strictement monotone sur I .gif)
f bijective de I sur l'image de I par f
Vrai Faux
Exercice "VRAI ou FAUX"sin-1(x)=.gif)
Vrai Faux
Sélection multiple
Sélection multiple
Exercice "VRAI ou FAUX"Pour toute fonction réelle f et pour tout réel a, on a:
f dérivable en x = a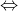
f'd(a) = f'g(a)
f dérivable en x = a
Vrai Faux
Exercice "VRAI ou FAUX"La derivée de 4x vaut ln(4).exln(4)
Vrai Faux